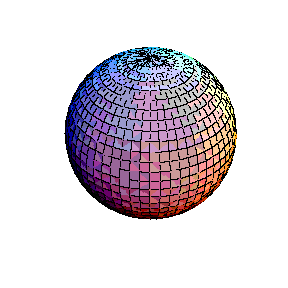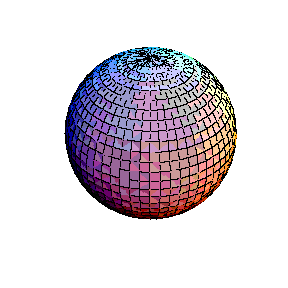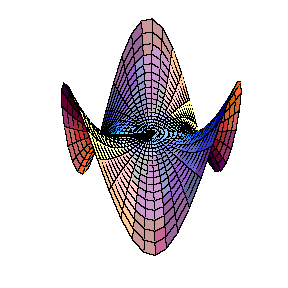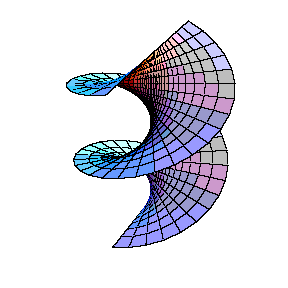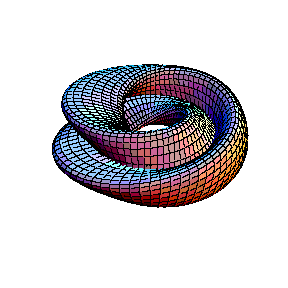Algumas notas sobre Superfícies em R³:
Curvatura
A curvatura (de Gauss) de uma superfície, é a medida
escalar da taxa de variação da direcção
dum vector normal unitário em torno da superfície.
Um plano tem curvatura zero: tem
direcção normal constante.
Uma esfera tem curvatura constante:
o seu vector normal unitário varia a uma taxa constante
em todos os pontos.

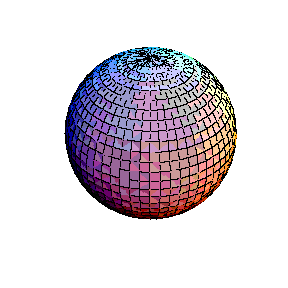
Convencionalmente, diz-se que uma esfera tem curvatura positiva
pois, qualquer que seja o ponto da esfera, ela encontra-se sempre
do mesmo lado do plano tangente a esse ponto.
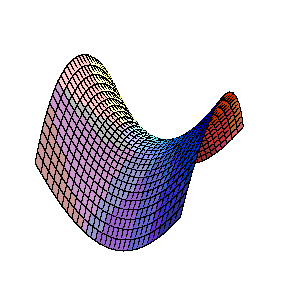
Numa sela, isto já não
acontece. Qualquer que seja o ponto da sela, a superfície
atravessa sempre o plano tangente em torno desse ponto e por isso
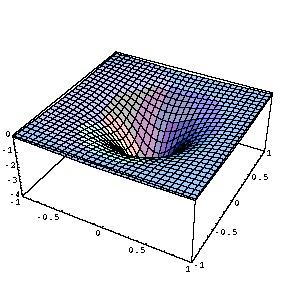
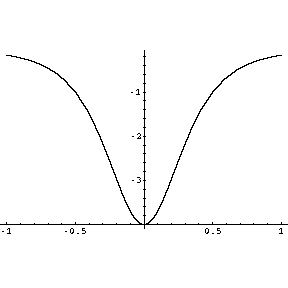
a curvatura é negativa. Aqui temos um exemplo simples dado
por z = x² - y², e a sua
curvatura. Podemos ver que a curvatura é igual a -4 na origem,
mas converge para zero à medida que nos afastamos desse ponto.
Existem superfícies de sela mais complicadas como podemos
ver no exemplo seguinte.
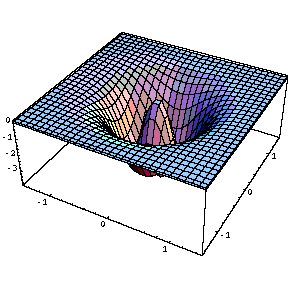
Monkey Saddle: z = x³
- 3x y²
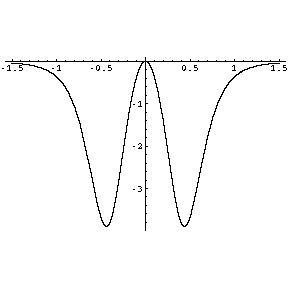
Aqui temos esta superfície e a sua curvatura. Note que
a curvatura na origem é nula, como podemos observar na secção
do gráfico da curvatura.
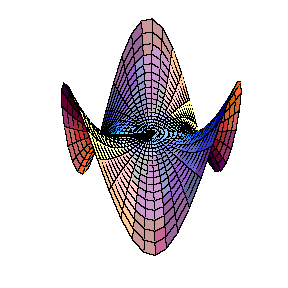
Sabemos então que uma esfera tem curvatura constante positiva
e que, numa sela, a curvatura é negativa. Assim, se quisermos curvatura
constante negativa, podemos esperar que em torno de qualquer ponto,
a superfície se pareça com uma sela. Ao contrário
da esfera, uma superfície deste tipo, não se fecha
nem é limitada. Exemplos famosos são a
Curvatura Média:
Para além da curvatura de Gauss, que é intrínseca
à superfície e não depende do modo como ela
está imersa no espaço, definimos também curvatura média num ponto. Para
este efeito, consideramos as curvas determinadas pela intersecção
da superfície com planos perpendiculares ao plano tangente
a esse ponto. Tomam-se depois os valores máximo e mínimo
das curvaturas destas curvas (curvaturas
principais). A curvatura média da superfície nesse
ponto é então a média destes dois valores. Eis aqui
alguns exemplos de como determinar as curvaturas principais:
Sela
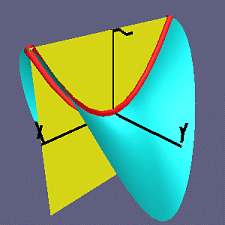
Clique sobre a imagem para obter uma rotação do
plano.
No filme, a curvatura principal maxima é a curvatura da curva
vermelha, e a mínima é a da curva azul.
Superfícies minimais são
as que possuem a menor área possivel entre as superfícies
com um dado bordo e por isso têm curvatura média nula.
As "superfícies de sabão" que se obtêm em estruturas
em arame, são superfícies minimais.
O que caracteriza uma superfície minimal é que em
torno de qualquer ponto, "curva" positivamente ao longo de uma dada
direcção principal e negativamente na direcção
perpendicular.
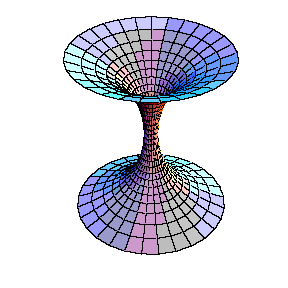
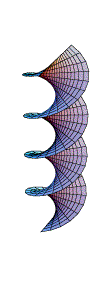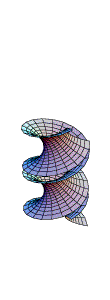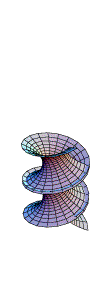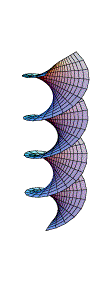
Aqui temos dois exemplos que podem ser transformados continuamente
um no outro através de uma família de superfícies
minimais: a helicóide e a catenóide.
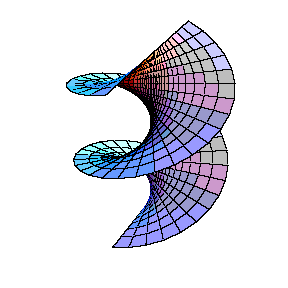
Novas superfícies a partir de outras:
Uma banda de Mobius pode ser construída
unindo as pontas de uma banda depois de a torcer. A superfície
resultante tem apenas uma aresta, um lado e é não-orientável
(não tem normal contínua).


Unindo as extremidades de um tubo ou cilindro obtemos um toro,
que é orientável


Unindo as extremidades de um tubo com orientações
opostas (o equivalente a torcer na banda de Mobius), dá
origem à garrafa de Klein, que pode ser mais facilmente vista
utilizando um tubo duplo:

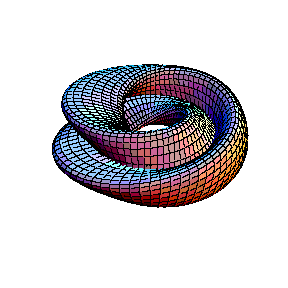
Garrafa de Klein: Superfície fechada não orientável
Os gráficos utilizados foram criados por C.T.J. Dodson,
UMIST utilizando Mathematica com funções do livro de
A. Gray, Modern Differential Geometry of Curves and Surfaces,
Second Edition, CRC Press, Boca Raton, 1997.
Os gráficos animados utilizam o software LiveGraphics3D
e foram criados pelo Geometry Center, University of Minnesota.