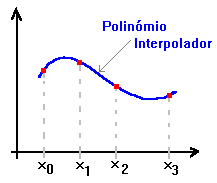
O polinómio de 3º grau interpola a função em 4 pontos
A interpolação consiste em determinar uma função (iremos considerar polinómios), que assume valores conhecidos em certos pontos (que chamaremos nós de interpolação). A classe de funções escolhida para a interpolação é a priori arbitrária, e deve ser adequada às caracteristicas que pretendemos que a função possua.
A interpolação polinomial pode-se revelar desadequada se os nós de interpolação não forem escolhidos convenientemente (o que leva ao uso de nós de Chebyshev...). De um modo geral, o conjunto das funções interpoladoras é determinado por um número finito de parâmetros (no caso dos polinómios, são os seus coeficientes...) que deverá ser igual ao número de condições impostas (ou seja, ao número de nós), para que haja apenas uma solução. Nos casos que veremos, a determinação dos parâmetros, que definem a função interpoladora, irá levar-nos à resolução de um sistema linear.
Se considerarmos a interpolação polinomial, podemos evitar
a resolução desse sistema, usando as fórmulas de Lagrange
ou de Newton, que reduzem significativamente o número de operações
envolvido.
Consideremos um conjunto de pontos (designados
nós de interpolação)
x0 , ... , xn , a que estão associados
os valores de uma função f0 , ... , fn,
respectivamente.
Pretendemos encontrar um polinómio p tal que
| p ( xi ) = fi |

Escrevendo p( x ) = a0 + a1 x + ... + am xm, obtemos o sistema
| a0 + a1 x0 + ... + am x0m = f0 |
| ... |
| a0 + a1 xn + ... + am xnm = fn |
| é
ê ê ê ê ë |
|
ù
ú ú ú ú û |
é
ê ê ê ê ë |
|
ù
ú ú ú ú û |
= | é
ê ê ê ê ë |
|
ù
ú ú ú ú û |
em que a matriz do sistema é conhecida como Matriz de Vandermonde.
A existência e unicidade do polinómio interpolador é
equivalente a assegurar que o
sistema é possível e determinado para quaisquer x0
, ... , xn distintos.
Teorema:
Dados n+1 nós, x0 , ... , xn
e os respectivos valores f0 , ... , fn,
existe um e um só, polinómio interpolador de grau
<n,
para esses valores.
dem:
Agora, basta considerar a Fórmula Interpoladora de Lagrange:
|
|
(a regra subjacente é que no denominador vai ficar a diferença entre os nós, que não são comuns às diferenças divididas do numerador).
Observação: Qualquer permutação da
ordem dos nós não altera o resultado.
Ou seja, por exemplo, f [ x1, x2 , x3
] =
f [ x2, x3 , x1 ]
Nota: Podemos considerar os valores fi como diferenças divididas de ordem zero, e reparamos que isso é coerente com a definição da diferença de 1ª ordem.
Resta determinar o valor do coeficiente Cn
.
Proposição: O coeficiente
Cn , que é o coeficiente do termo xn do polinómio
interpolador pn
(nos nós x0 , ... , xn), é
a diferença dividida f [ x0 , ... , xn
].
dem:
Consideremos os polinómios interpoladores
pn-1 que interpola os nós x0
, ... , xn-1 com coeficiente Cn-1
qn-1 que interpola os nós x1
, ... , xn com coeficiente C*n-1
Reparamos que definindo
| q(x) = | (x - x0) qn-1(x) -(x
- xn) pn-1(x)
(xn-x0) |
Fórmula de Newton
Portanto, podemos agora escrever
e podemos obter sucessivamente, a partir do polinómio interpolador de grau zero p0(x) = f0 :
| p1(x) = f0 + f [ x0 , x1 ] ( x - x0) |
| p2(x) = f0 + f [ x0 , x1 ] ( x - x0) + f [ x0 , x1, x2 ] ( x - x0) ( x - x1) |
| ... etc ... |
| pn(x) = f0 + | n
S k=1 |
f [x0 , ... , xk] (x - x0 ) ... (x - xk-1) |
Número de operacões:
Se resolvermos o sistema linear, como vimos no Capítulo II,
é necessário efectuar um total de ~2 n3/3 operações.
Usando a Fórmula de Lagrange ou a Fórmula de Newton reduzimos
para ~3 n2/2. A F. Lagrange usa mais multiplicações+divisões
que a F. Newton, que, por sua vez, usa mais somas+subtracções.
O erro de interpolação, num certo ponto x, é :
É claro, que se x fôr um dos nós, o erro é zero! Caso contrário, podemos considerar esse valor x como um novo nó, e pensar no polinómio interpolador pn+1 . Já vimos que
Considerando y = x, e como x é um novo nó de interpolação, pn+1( x ) = f ( x ), e obtemos :
f( x ) = pn( x ) + f[ x0 , ... , xn, x ]( x - x0 ) ... ( x - xn )
|
|
Esta fórmula é útil do ponto vista teórico,
como também veremos mais tarde, no caso da integração.
Vamos, no entanto, aproveitar uma relação entre as diferenças
divididas e as derivadas, para estabelecer uma outra fórmula.
Teorema :
Consideremos n+1 nós de interpolação x0
, ... , xn distintos entre si,
incluídos no intervalo [x0 , xn],
onde a função f é de classe
Cn.
Então
| $x em ]x0 , xn [ : f [x0 , ..., xn] = | f(n)(x)
n! |
Este teorema pode ser aplicado à fórmula do erro anterior, e obtemos o seguinte corolário:
Corolário :
Seja V um intervalo que contenha os nós x0 , ...
, xn e ainda o ponto x.
Se a função f fôr de classe Cn+1(
V )
então temos a seguinte fórmula para o erro de interpolação:
| $x em V : en(x) = | f(n+1)(x)
(n+1)! |
n
P k=0 |
(x - xk ) |
Terminamos este parágrafo, com um exemplo de uma função
em que a aproximação, por interpolação polinomial,
pode conduzir a maus resultados.
Com efeito, se considerarmos a função f (x) =
(1 + 25 x2 )-1, e pensarmos em interpolá-la
no intervalo [-1, 1], usando nós igualmente espaçados, ao
aumentarmos o número de nós, em vez de obtermos uma melhor
aproximação, vamos obter uma aproximação cada
vez pior, nas extremidades do intervalo!
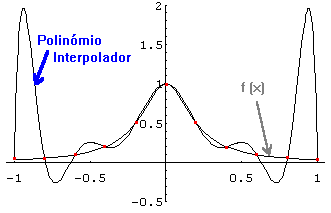
Exemplo de Runge: f(x) = (1 + 25 x2 )-1
usando 11 nós de interpolação igualmente espaçados
Este problema pode ser resolvido, escolhendo nós de interpolação adequados (nós de Chebyshev).
Nós de Chebyshev
Como o erro de interpolação é dado por en
( x ) = f [ x0 , ... , xn, x ] ( x - x0
) ... ( x - xn ), se a parte relativa à diferença
dividida varia com a função, e não pode ser controlada
a priori, a parte relativa ao produto dos termos, ou seja,
|w(x)| = |( x - x0 ) ... ( x - xn )|
poderá ser minimizada para certos nós x0,...,xn
tendo como objectivo a aproximação num intervalo específico.
Iremos considerar o intervalo [-1,1].
A solução que minimiza o valor de w(x) é dada
pelos nós de Chebyshev, que são os zeros dos polinómios
de Chebyshev:
Como |Tn+1(x)| < 1, concluímos que