Métodos Iterativos para Equações Não Lineares

Pretendemos aproximar soluções (também designadas como raízes) de equações da forma :

f ( x ) = 0
onde f deverá ser, pelo menos, uma função contínua numa vizinhança da raiz.

Se resolver uma equação linear ax+b=0 é trivial, o mesmo já não se passa se considerarmos uma função f mais complicada. Comecemos por considerar, por exemplo, as equações x4 - 4 x3 - x + 5 = 0 ou 2 ex - x sin(x+3) = 0.
São ambas equações não lineares. No primeiro caso, apesar de existir uma fórmula resolvente geral, é complicada, e no segundo caso não existe. Para este tipo de equações temos, no entanto, a possibilidade de encontrar soluções usando métodos iterativos simples.
Um método iterativo, consiste de um modo geral, numa aproximação inicial

x0, também designada iterada inicial,

e num processo de obter sucessivamente novas iteradas
xn+1 a partir das anteriores xn, ...

Desta forma, pretendemos obter uma sucessão que convirja para z, solução da equação f(x)=0, também designada por raiz da equação, ou zero da função f. Começamos por rever alguns resultados base.

Localização de Raízes

Traçando o gráfico da função, podemos ter uma ideia aproximada da localização das raízes, mas para assegurarmos rigorosamente que, num intervalo, existe uma e uma só raiz, recordamos alguns teoremas elementares da análise:

Teorema (do Valor Intermédio):
Seja f uma função contínua no intervalo [a,b].
Se f(a) f(b) < 0 então existe pelo menos uma raiz da equação f(x) = 0 no intervalo [a,b].

O teorema do valor intermédio garante apenas a existência. Para garantirmos a unicidade, podemos usar :

Teorema (de Rolle) :
Seja f ÎC1[a,b]. Se f ' (x) ¹ 0, "xÎ[a,b], então existe no máximo um  z Î]a,b[ :  f(z) = 0.
(podemos garantir a unicidade, num caso mais geral, desde que a função f seja estritamente monótona).

É ainda importante referir que usando apenas o teorema do valor médio de Lagrange podemos obter um processo muito simples para obter uma estimativa de erro para um valor aproximado da raiz pretendida.

Teorema (do Valor Médio de Lagrange):
Seja f ÎC1[a,b]. Então

$xÎ]a,b[:  f(b) - f (a) = f ' (x)(b - a)

Corolário (Estimativa elementar de erros de raízes):
Seja f ÎC1[a,b], e seja z~ a aproximação da raiz pretendida z.
Então

 |z - z~| < |f (z~)| / minxÎ[a,b] |f ' (x)|
dem:
Basta reparar que, como f (z) = 0 temos  f(z~) = f(z~) - f (z) = f ' (x)(z~ - z).
Portanto z~ - z = f(z~) / f ' (x) e daqui conclui-se o resultado.



Observação:
Estes teoremas não nos dão um método para aproximar a solução do problema, no entanto, podemos nos basear no teorema do valor intermédio para desenvolver um método iterativo muito simples:
MÉTODO da BISSECÇÃO. Sabendo que no intervalo [a, b] a equação f(x) = 0 tem apenas uma e uma só raiz , vamos construir
intervalos [ an, bn ] com metade do comprimento dos anteriores, onde asseguramos a existência da raiz.
O método pode-se esquematizar num ciclo :
Intervalo Inicial : [ a0, b0 ] = [ a, b ]
Repetir :  1) xn+1 = ( an + bn) / 2 
2) Se f (xn+1) f(an) < 0 
Então an+1 = an; bn+1 = xn+1 
Senão an+1 = xn+1; bn+1 = bn
Até que :
f(xn+1) = 0 ou |xn+1-xn| < e
Usamos o critério de paragem |xn+1-xn| < e onde o valor e>0 é um valor suficientemente pequeno pois neste caso o erro absoluto verificará | en+1 | < ½ |an - bn| = |xn+1 - xn| < e.
Para além disso, podemos determinar facilmente um majorante do erro para uma iterada xn a partir do comprimento do intervalo inicial:
| en| < ½ |an-1 - bn-1| = (1 / 2)n | a0 - b0|

MÉTODO do PONTO FIXO

É talvez o método mais simples e encontra-se na base de outros métodos. A ideia principal consiste em estabelecer uma equivalência adequada:

f(x) = 0   Û   x = g(x)
e a partir daqui,
Escolher uma iterada inicial x0
Iterar xn+1 = g(xn )

Considerando g contínua, se o método convergir, converge para um certo z (a que chamamos ponto fixo de g ) tal que:

z = g(z)
este ponto z, pela equivalência estabelecida, será uma raiz da equação, ou seja f(z) = 0.

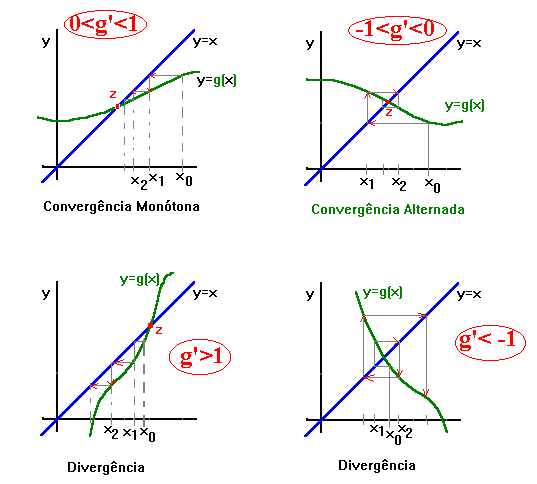
Geometricamente, podemos ter as seguintes situações:

.

Definição:
Uma função g contínua em [a, b] diz-se Lipschitziana se existir um L > 0 tal que :

| g(x) - g(y) | < L | x - y | ,   " x, y Î [a, b]

Se L < 1 a função diz-se Contractiva.

Proposição:
Se g é uma função diferenciável em [a, b], e temos |g'(x)| < L < 1, para x em [a, b], então a função g é contractiva nesse intervalo.

dem:
Usando o T. Lagrange, sabemos que, para quaisquer x, y em [a,b]

| g(x) - g(y) | = |g'(x)| |x-y| , para um certo x em ]x, y[ Ì [a, b]
concluimos, aplicando a hipótese.

Teorema (do ponto fixo num intervalo limitado).
Seja g uma função contínua em [a, b].
Se g for contractiva em [a, b], e se g([a, b]) Ì[a, b] , então:

dem:
  • Existência (de ponto fixo)
    • Consideramos uma função auxiliar h(x) = g(x) - x , contínua,
    como g([a, b]) Ì [a, b] temos g(a) > a, g(b)< b assim h(a) h(b) < 0.
    Logo, pelo T.Valor Intermédio, existe um z : h(z) = 0, ou seja g(z)=z.
  • Unicidade (do ponto fixo)
    • Supondo que g é contractiva e z e w são pontos fixos de g em [a,b] , temos:
    | z - w | = | g(z) - g(w) | < L |z - w|,
    logo (1 - L) | z - w | < 0 e como L < 1 podemos concluir que | z - w |=0, ou seja, z=w.
  • Convergência
    • É fácil ver por indução que se x0 pertence a [a,b], qualquer xn também pertence.
    Basta reparar que xn+1= g(xn) e que g([a, b]) Ì [a, b] .
    Por outro lado, temos | z - xn+1 | = | g(z) - g(xn) | < L | z - xn |
    Logo | z - xn+1 | < Ln+1 | z - x0 | ® 0, pois L < 1 e temos | z - x0 | < | a - b | 


    Corolário:
    Seja g uma função C1( [a, b] ).
    Se

  • g([a, b]) Ì [a, b],
  • L = max[a,b] | g'(x) | < 1

    • então as condições do T. Pto. Fixo são verificadas e temos:
  • g tem um e um só ponto fixo z em [a,b]
  • A sucessão xn+1 = g(xn) converge para esse ponto fixo z, dado qualquer x0 em [a, b].


    • Observação:
    Para além disto, nas condições do Teorema do Ponto Fixo, temos :
  • Se 0 < g'(x) < 1 então a convergência é monótona (ou seja, as iterações ficam todas à direita [à esquerda] da raiz, se a iterada inicial estiver à direita [à esquerda] da raiz).
  • Se -1 < g'(x) < 0 então a convergência é alternada (ou seja, as iterações vão ficar alternadamente à esquerda e à direita da raiz)

    •  

     

    Nota: Portanto, no caso de asseguramos convergência alternada, sabemos que a raiz irá sempre pertencer a intervalos em que os extremos são xn e xn+1.

    Teorema (Divergência):
    Seja g uma função diferenciável tal que | g'(x) | > 1 em [a,b].
    Neste caso, a sucessão xn+1= g(xn) não pode convergir para
    um ponto fixo z de g situado nesse intervalo (a única excepção
    será se, numa certa iterada, obtivermos "acidentalmente" o ponto fixo z ).

    Teorema (Convergência Local):
    Seja z um ponto fixo de g, função diferenciável numa vizinhança de z,
    tal que |g'(z)|<1, então a sucessão xn+1=g(xn) converge para z,
    desde que x0 esteja suficientemente próximo de z.

    Definição (Ordem de Convergência):
    Consideremos uma sucessão (xn) convergente para z. Ao valor p tal que:

      lim
    m ® ¥    		  |em+1| 
      |em| p    		  = K¥  (com 0 < K¥ < ¥ )

    chamamos ordem de convergência, e ao valor K¥ chamamos coeficiente assimptótico de convergência.

  • Se p = 1 a convergência diz-se linear.
  • Se p = 2 a convergência diz-se quadrática.
  • De um modo geral, se p > 1, a convergência diz-se supra-linear.


    • Proposição :
    Nas condições do teorema do ponto fixo, a convergência é linear
    se g'(z) ¹ 0 e o coeficiente assimptótico de convergência é |g'(z)|.
    dem:
    Usando o Teorema de Lagrange, sabemos que

    | xm+1 - z | = | g(xm) - g(z) | = | g'(cm) | | xm - z |

    com cm num intervalo aberto cujos extremos são xm e z.
    Logo, dividindo e passando ao limite, temos:

      lim
    m ® ¥    		  |em+1| 
      |em|    		   lim
    m ® ¥    		  |z - xm+1| 
      |z - xm|    		  = |g'(z)| = K¥

    pois cm tende para z, já que o extremo xm do intervalo tende para z. Como suposemos que g'(z) ¹ 0, concluimos o teorema.

  • Podemos agora perguntar qual será a ordem de convergência quando g'(z)=0. O teorema seguinte dá-nos a resposta:

    •  

     

    Teorema (Convergência Supra-Linear):
    Seja g uma função C p( I ), onde I é um intervalo que é uma vizinhança de z, ponto fixo de g, com p > 2.
    Se g'(z) = ... = g(p-1)(z) = 0 com g(p)(z) ¹ 0, então:

      lim
    m ® ¥    		  |em+1| 
      |em| p    		  =   |g(p)(z)| 
       p!

    ou seja, o método do ponto fixo tem convergência de ordem p.

    MÉTODO de NEWTON

    Pode ser encarado como um caso particular do método do ponto fixo, onde é possível obter uma convergência quadrática.
    Basta reparar que se f '(x) ¹ 0:

    f(x) = 0 Û x = x - f(x) / f '(x)

    definindo a função iteradora g(x) = x - f(x) / f '(x), e os pontos fixos de g serão os zeros de f.
    Para além disso, podemos ver que :

    g'(x) = f(x) f ''(x) / ( f ' (x) )2

    ora como f(z) = 0 então g'(z) = 0 . Pelo teorema anterior, usando esta função iteradora g, é possível arranjar uma vizinhança da raiz onde asseguramos, pelo menos, uma convergência quadrática (desde que f ' (z) ¹  0).

    Portanto o método de Newton resume-se a efectuar as iterações:

    Iterada inicial: x0
    xn+1 = xn - f(xn ) / f ' (xn )

    Historicamente, a origem do método de Newton é geométrica. Consiste em definir a nova iterada a partir da intersecção com o eixo das abcissas da tangente à função f (calculada na iterada anterior) :

    basta reparar que a equação da tangente num ponto xn é
    y = f(xn ) + f ' (xn ) ( x - xn )
    e a iterada xn+1 é a "raiz da tangente", basta pois fazer y = 0 para verificarmos que o valor de xn+1 coincide com o obtido.

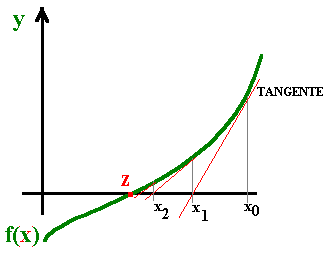
    É também claro, mesmo geometricamente, que não podemos ter iteradas em que f ' (xn) = 0, pois ficariamos com tangentes paralelas ao eixo das abcissas, que nunca o intersectariam...

    Para assegurar a convergência, podiamos aplicar o teorema do ponto fixo à função g do método de Newton, mas podemos estabelecer um critério mais simples :

    Teorema (Condições Suficientes de Convergência para o Método de Newton):
    Seja f uma função C2[a, b] que verifique :

    1) f(a) f(b) < 0
    2) f ' (x) ¹  0 para qualquer x em [a,b]
    3) f ''(x) > 0 ou f ''(x) < 0 para qualquer x em [a,b]
    4) f(x0 ) f ''(x) > 0 para qualquer x em [a, b]

    então a equação f(x) = 0 tem uma solução única z Î[a,b] e o método de Newton
    converge monótona e quadraticamente para essa solução (para os x0 que verificarem 4)).

    Se a condição

    4') | f(a) / f '(a) | < | a - b | e | f(b) / f '(b) | < | a - b |

    for verificada então x1 verifica 4) havendo convergência "x0Î[a,b].

    Fórmula do Erro do Método de Newton
    Obtém-se, facilmente, através do desenvolvimento em série de Taylor (em torno de xn):

    f(z) = f(xn) + f'(xn ) (z - xn) + ½ f''(xn ) (z - xn )2
    para um certo xn no intervalo aberto cujos extremos são z e xn.

    Dividindo por f ' (xn ), não nulo, ficamos com:

    0 =   f (xn)
     f ' (xn)    		 + z - xn +   f '' (xn)
     2 f ' (xn)    		 (z - xn )2

    portanto

    en+1 = -   f '' (xn)
     2 f ' (xn)    		  (en )2

    Se tivermos assegurado as condições de convergência num intervalo [a,b], podemos garantir a priori

    |en+1 | <  max  |f '' (x)|
     2 min | f ' (x)|    		  (en )2

    Proposição: (Convergência Local)
    Seja f uma função C2( I ), onde I é um intervalo que é vizinhança da raiz z.
    Se f '(z) ¹ 0, então a sucessão definida pelo método de Newton converge para z (desde que x0 seja suficientemente próximo de z ), e a convergência é quadrática,

      lim
    m ® ¥    		  |em+1| 
      |em| 2    		  =   | f '' (z)|
     2 | f ' (z)| 

    Observação:
    Nos casos em que f(z) = f '(z)=0, o que corresponde a casos de raizes duplas, há ainda a convergência do método de Newton, mas essa convergência será apenas linear.

    MÉTODO da SECANTE

    Apresentamos agora o método da secante, análogo ao método de Newton, mas substitui o cálculo das derivadas pelo cálculo de uma razão incremental. Geometricamente, corresponde a substituir o papel da tangente, no método de Newton, por uma secante (de onde vem o nome). Para definir a recta secante vamos precisar sempre de dois pontos, o que implica que tenhamos que considerar duas iteradas iniciais, que designamos por x-1 e x0.
    As vantagens do método da secante face ao método de Newton residem essencialmente em evitar o cálculo da derivada, o que nas mais frequentes situações pode ser uma tarefa morosa ou mesmo impraticável. Em termos de ordem de convergência é apenas ligeiramente menos eficaz que o método de Newton, mas isso é compensado pelo facto de cada iteração prescindir do cálculo da derivada, tornando-se assim normalmente mais rápido que o método de Newton.

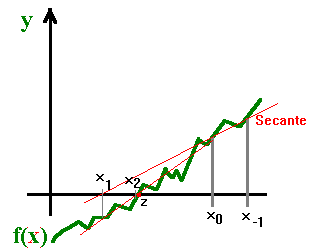
    De forma semelhante à que fizemos no método de Newton, calculando agora o ponto de intersecção da secante com o eixo das abcissas, obtemos a fórmula para xn+1, e o método da secante fica:

    Iteradas iniciais: x-1 ,  x0
    Iterar:
    xn+1 = xn - f ( xn )   xn - xn-1
     f(xn) - f(xn-1)

    Condições Suficientes de Convergência: São idênticas às enunciadas para o Método de Newton.
    Apenas a condição 4) deverá ser substituída por

    4* ) f(x0 ) f ''(x) > 0 e também f(x-1 ) f ''(x) > 0 para qualquer x em [a, b]

     

     

    Fórmula do Erro :

    en+1 = -   f '' (xn)
     2 f ' (hn)    		  en en-1  para xn , hn no intervalo contendo {z , xn , xn-1}

    Neste caso a ordem de convergência é supra-linear mas não é quadrática, mas, como já referimos, isto não impede que normalmente seja bastante mais eficaz que o método de Newton, devido a prescindir de calcular a derivada.
    ( Usando logaritmos, e o facto que o limite da razão de uma sucessão de Fibonacci é o número de ouro p=1.61803... podemos verificar que a ordem de convergência dá exactamente este valor.)