Métodos
Iterativos para Sistemas Não Lineares
Método do Ponto
Fixo em Rn
Iremos agora ver uma generalização do método e
do teorema do ponto fixo para dimensão n (é ainda possível
generalizá-lo a espaços de dimensão infinita, considerando
espaços funcionais adequados).
Consideremos, por exemplo, um sistema da forma:
| x1 - x2 sin ( x1 ) = 0 |
| x1 - x2 + cos ( x1 x2 )
= 0 |
que se pode escrever na forma mais geral F(x) = 0
com F : Rn ®
Rn .
Neste exemplo, temos:
F1(x1, x2) = x1 - x2
sin ( x1 )
F2(x1, x2) = x1 - x2
+ cos ( x1 x2 )
De forma análoga ao caso unidimensional, podemos pensar num Método
do ponto fixo para Rn, começando por estabelecer
a equivalência:
F ( x ) = 0 Û
x = G ( x )
No nosso exemplo, poderiamos escrever:
x1 = x2 sin ( x1 ) = G1( x1,
x2 )
x2 = x1 + cos ( x1 x2 )= G2(
x1, x2 )
Temos assim definida uma função iteradora
G e obtemos
um método do ponto fixo :
| Iterada inicial: x(0) |
| Iterar x(n+1) = G ( x(n)) |
semelhante ao caso unidimensional.
Para estabelecermos as condições de convergência
vamos, de novo, definir a contractividade, agora em Rn.
Definição:
Seja G : W ÍRn®
Rn.
Se existir L<1 : ||G(x) - G(y) || < L || x -
y || para quaisquer
x, y em W,
então diz-se que G é contractiva em W
relativamente à norma ||.|| .
Teorema: ( do Ponto Fixo em Rn
)
Seja W um conjunto fechado e G :
WÍ
Rn ®
Rn,
tal que
(i) G(W) ÍW
,
(ii) G é contractiva em W,
então existe um e um só ponto fixo z ÎW,
e o método do ponto fixo converge para z, se
x(0)ÎW.
dem:
Vamos só ver o caso em que W é
limitado, por simplicidade (a demonstração geral é
semelhante).
É claro que se x(0) pertencer a W,
atendendo à hipótese (i) e como x(n+1)
= G( x (n)),
teremos todos os elementos da sucessão, x(n),
em W.
Isto é importante para aplicarmos a contractividade, e assim mostrarmos
que x(n) é uma sucessão de Cauchy:
||x(n+m) - x(n) || = ||G ( x(n+m-1))
- G ( x(n-1)) ||
< L ||x(n+m-1)
- x(n-1) || < ... < Ln
||x(m) - x(0) || ®
0
quando m, n tendem para infinito, já que L < 1, e porque
||x(m) - x(0) || é limitado,
já que os termos da sucessão estão em W,
que assumimos ser limitado.
Concluimos assim que é uma sucessão de Cauchy num conjunto
fechado, logo o limite z pertence a W.
É fácil ver que z é o ponto fixo, porque :
||x(n+1) - G( z ) || = ||G(x(n))
- G( z ) || < L ||x(n) - z ||
----> 0 ou seja, como x(n) converge para o limite z
isto implica que x(n) converge também para G(
z ). Logo z = G ( z ) .
A unicidade do ponto fixo surge por absurdo, já que se existissem
dois pontos fixos distintos z, w em W,
então:
||z - w || = ||G(z) - G( w ) || <
L ||z - w ||
ora se eles são distintos podemos dividir por ||z - w
|| e obtemos L > 1 , o que contradiz a hipótese de contractividade!
Corolário: Da demonstração
anterior podemos deduzir as seguintes majorações para os
erros:
|| e(n) || < L || e(n-1) ||
|| e(n) || < 1/( 1 - L ) ||
x(n+1) - x(n) ||
etc...
Observação:
O caso dos métodos iterativos para sistemas lineares, que vimos,
podem ser englobados neste contexto considerando
x = G (x) = M-1b - M-1N x
Para exigir que G seja contractiva, como
|| G ( x ) - G ( y )|| = || M-1b + C x - (M-1b
+ C y)|| =
= || C ( x - y ) || < ||C|| || x - y
||
basta que ||C|| < 1, condição que já tinhamos
obtido.
Finalmente, notamos que, como Rn é fechado,
podemos aplicar o teorema do ponto fixo para um qualquer x(0)
em Rn.
Para verificarmos que uma função é contractiva,
não é necessário usar sempre a definição.
Tal como no caso unidimensional, em que utilizamos a derivada, podemos
aqui estabelecer uma condição suficiente, mais simples, que
envolve agora a noção de matriz Jacobiana:
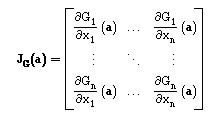
Teorema:
Seja W um conjunto fechado e convexo
em Rn, e seja
G uma função C1(W).
Se ||JG(x)|| < L < 1, para qualquer
x
em W,
então a função G é contractiva em
W,
para a norma ||.||.
Observação:
A determinação dos domínios de convergência,
para uma certa função iteradora, constitui ainda hoje um
problema em aberto, devido à complexidade inerente. Para termos
uma ideia dessa complexidade, basta pensar numa função iteradora
G
extremamente simples:
G1(x,y) = x2 - y2+c1
G2(x,y) = 2 x y + c2
que corresponde a iterar, nos complexos, zn+1 = zn2
+ c .
Se considerarmos, por exemplo, c = 0.3 - 0.4 i, o domínio
de iteradas inicias z0, para as quais a sucessão (zn)
é limitada define um conjunto fractal (chamado conjunto de Julia)...

Método de Newton Generalizado
De forma análoga ao que fizemos no caso unidimensional, podemos
deduzir aqui um método, inspirado no método de Newton, cuja
ordem de convergência é usualmente quadrática.
Pretende-se resolver F ( x ) = 0 e reparamos que se pode estabelecer,
numa vizinhança da solução, a equivalência
F ( x ) = 0 Û x = x
- JF-1( x ) F ( x )
bastando para isso que a função vectorial F seja de
classe C1 e que det [JF( x )] ¹
0, nessa vizinhança.
Podemos assim definir uma função iteradora
G( x ) =
x - JF-1( x ) F ( x ) a que aplicamos o método
do ponto fixo.
Para evitar o cálculo "pesado" da inversa da matriz jacobiana, podemos
fazer uma pequena alteração no método, de forma a
substituirmos o cálculo da inversa pela resolução
de um sistema.
O método de Newton generalizado fica então :
|
Iterada inicial: x(0)
|
|
Determinar d, resolvendo o sistema linear
|
|
x(k+1) = x(k) + d
|
Observação:
i) A convergência do método de Newton, quando det
[JF( z )] ¹ 0, é
quadrática, tendo-se:
|| z - x(k+1) || < K || z - x(k)
||2
para uma certa constante K>0.
ii) Quando a resolução do sistema é morosa, utiliza-se
também uma modificação deste método, aplicando
a estratégia de não actualizar constantemente a matriz jacobiana,
guardando a sua factorização durante algumas iterações,
o que reduz o número de operações na resolução
do sistema.


