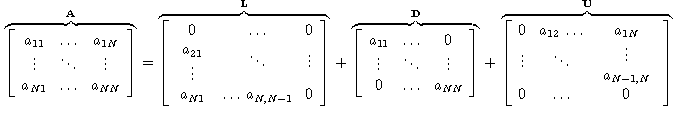
onde L é a matriz triangular inferior, U a matriz triangular superior, ambas com zeros na diagonal principal e D a matriz diagonal.
Neste parágrafo, o objectivo é encontrar métodos que permitam aproximar a solução de um sistema linear, de forma a diminuir o número de operações (relativamente aos métodos directos), o que pode ser útil no caso de se tratar de um sistema com um grande número de equações, especialmente se a matriz possuir muitos elementos nulos. Outra utilidade é evitar definir ou armazenar a matriz, ou ainda, evitar os problemas de instabilidade numérica, que podem ocorrer num método directo.
Consideremos um sistema genérico A x = b
escrito
na forma A = M + N.
Supondo que M é invertível, obtemos
Daqui podemos retirar um método iterativo que consiste em:
| Escolher um vector inicial x(0) |
| Iterar x(k+1) = M-1b - M-1 N x(k) |
É importante que a matriz M seja muito mais simples do
que A, porque senão não estariamos a simplificar o
problema...
Note-se que esta iteração pode ser feita de outra forma,
não havendo necessidade de se proceder verdadeiramente ao cálculo
da inversa de M.
De entre os métodos iterativos, iremos abordar os seguintes
métodos:
Consideramos a matriz A decomposta na soma de três matrizes
A
= L + D +U,
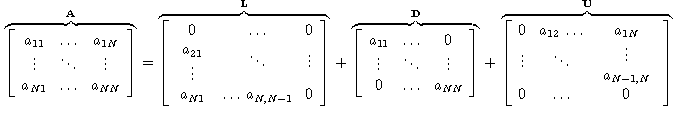
onde L é a matriz triangular inferior, U a matriz
triangular superior, ambas com zeros na diagonal principal e D a
matriz diagonal.
Notamos que a matriz diagonal D não deverá
ter zeros na diagonal principal.
Caso isso aconteça, deve-se efectuar uma troca de linhas ou
colunas na matriz A, para obtermos uma matriz D adequada.
| Iterada inicial x(0) |
| Iterar x(k+1) = D-1b - D-1 (L + U) x(k) |
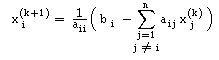
| Iterada inicial x(0) |
| Iterar x(k+1) = D-1b - D-1 L x(k+1) - D-1 U x(k) |
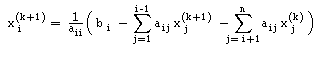
Vamos agora estabelecer critérios que nos permitam determinar
quando existe convergência para estes métodos iterativos.
Começamos por reparar que
|
|
ou seja, o erro convergirá para o vector nulo (para uma qualquer
iterada inicial)
se as sucessivas potências da matriz C tenderem para a
matriz nula.
Observação:
Se existir uma norma induzida ||.|| : ||C|| < 1 então
é claro que que isso se irá verificar,
porque ||e(k) || = || Ck e(0) ||
<
|| C ||k ||e(0) || ®
0, quando k tende para infinito,
qualquer que seja o e(0) , fixo pela iterada inicial.
Teorema : ( Condições
Necessárias e Suficientes de Convergência )
Os métodos iterativos convergem, qualquer que seja o vector
inicial x(0) ,
sse r(C)<1.
Notando que:
Critérios Suficientes de Convergência
Para além do teorema, que nos dá condições necessárias e suficientes de convergência, existem critérios mais simples que asseguram a convergência para qualquer iterada inicial. No entanto, essas condições, que iremos deduzir, são apenas condições suficientes.
Repare-se, por exemplo, no caso do método de Jacobi. Como C = D-1 ( L + U )
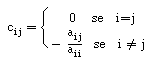
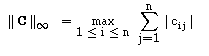
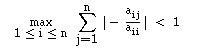

De forma análoga (usando uma norma semelhante à das colunas), podemos concluir que se
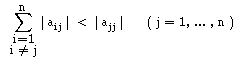
Este raciocínio pode-se aplicar também ao método
de Gauss-Seidel e obtemos :
Teorema : ( Condição
Suficiente de Convergência )
Se a matriz A tiver a diagonal estritamente dominante por linhas
ou por colunas, os métodos de Jacobi e de Gauss-Seidel convergem,
para qualquer vector inicial x(0) escolhido.
Nos casos dos métodos que estudamos, normalmente M está "mais próxima" de A no caso do Método de Gauss-Seidel (M = L + D ) do que no caso do Método de Jacobi ( M = D ).
Portanto, habitualmente o método de Gauss-Seidel converge mais rapidamente. Há, no entanto, casos em que isso não acontece, e um método pode convergir e o outro não!
Número de Operações: A menos que
as matrizes possuam zonas apreciáveis com elementos nulos, ambos
os métodos iterativos exigem um cálculo total de
~2n2
operações, por cada iterada, o que implica que, se forem
necessárias mais que ~n/3 iterações, exigimos
mais operações do que num método directo.
Portanto, o método consiste em
| Iterada inicial x(0) |
| Iterar x(k+1) = (1-w) x(k) + w D-1(b - Lx(k+1) - U x(k) ) |
e os seguintes teoremas dão-nos resultados acerca da convergência.
Teorema (Kahan - condição
necessária)
Para que haja convergência do método SOR, qualquer que
seja a iterada inicial,
é necessário que w esteja
em ]0,2[.
Teorema (Ostrowski-Reich - condição
suficiente)
Se a matriz A for simétrica e definida positiva, e considerarmos
w
em ]0,2[,
há convergência do método SOR, qualquer que seja
a iterada inicial.
Observação: Em particular, conclui-se que no caso em que A é simétrica e definida positiva o método de Gauss-Seidel converge.