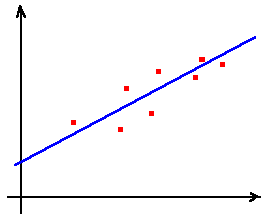
Regressão Linear: Neste caso pretendemos encontrar a função do tipo a + b x
(... ou seja, a recta) que "melhor se adapta" aos valores dados.
Neste parágrafo vamos estudar a aproximação de funções numa perspectiva diferente da interpolação. Por exemplo, se tivermos apenas os valores da função em certos pontos, não vamos exigir que a função aproximadora interpole a função dada nos pontos. Exigimos apenas que essa função aproximadora tome valores (nesses pontos) de forma a minimizar a distância aos valores dados... falamos em minimizar, no sentido dos mínimos quadrados!
Isto é importante em termos de aplicações, já que podemos ter valores obtidos, experimentalmente, com uma certa incerteza. Ao tentar modelizar essa experiência, com uma certa classe de funções, seria inadequado exigir que a função aproximadora interpolasse esses pontos.
Um caso simples, em que se aplica esta teoria é o caso da regressão linear, em que tentamos adaptar a um conjunto de pontos e valores dados, a "melhor recta", que (neste caso) será a recta que minimiza a soma quadrática das diferenças entre os valores dados ao valores da recta, nesses pontos.

Esta é uma perspectiva discreta, em que o conjunto
de valores dados é finito.
Podemos também pensar num caso contínuo,
em que apesar de conhecermos a função, não apenas
em certos pontos, mas em todo um intervalo, estamos interessados em aproximar
essa função (... no sentido dos mínimos quadrados)
por funções de uma outra classe, mais adequada ao problema
que pretendemos resolver. Por exemplo, podemos estar interessados em determinar
qual a "melhor recta" que aproxima a função sin(x)
no intervalo [0, 1] ...
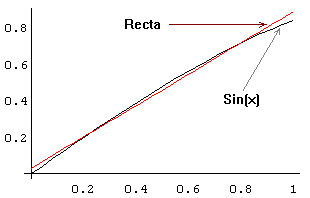
A recta que melhor aproxima sin(x) no intervalo [0,1],
no sentido dos mínimos quadrados
Temos que considerar agora uma classe de funções, entre as quais vamos tentar encontrar a que "melhor aproxima" aquele conjunto de valores, nos pontos dados.
Vamo-nos concentrar em funções da forma:
Neste caso, apenas teremos que determinar os parâmetros a0
, ... , an , de forma a que a soma quadrática das diferenças
entre os f( xi ) e os g( xi ) seja
mínima.
Faz pois sentido introduzir a distância || f - g || em
que
| || u ||2 = | n
S i=0 |
u( xi )2 |
| ( u, v ) = | n
S i=0 |
u( xi ) v( xi ) |
A norma e o produto interno estão bem definidos para funções
que assumem quaisquer valores
nos pontos x0 , ... , xn. Convém-nos trabalhar
com estas noções, já que aquilo que iremos ver, de
seguida, será exactamente igual no caso contínuo,
apenas a norma e o produto interno serão diferentes (substituiremos
o somatório por um integral...).
Pretende-se pois encontrar os parâmetros a0 , ... , an que minimizem a distância entre f e g , ou, o que é equivalente, minimizem :
Para obtermos esse mínimo, começamos por procurar os valores a0 , ... , am tais que todas as derivadas parciais de Q sejam nulas, isto é:
Calculamos a derivada parcial, usando as propriedades da derivação do produto interno :
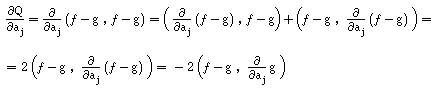
Por outro lado
Podemos ainda substituir a expressão de g e obtemos um sistema linear :
|
designado por sistema normal, que escrevemos matricialmente :
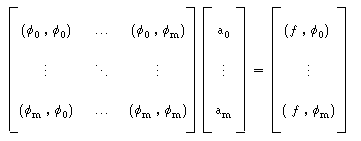 |
Teorema: Se as funções base f0
, ... , fm forem linearmente independentes,
a matriz do sistema normal é definida positiva.
dem:
Seja S a matriz do sistema e v um vector não nulo.
Temos (Sv)i = (f0,
fj
)v0 +...+(fm,
fj
) vm = (f0 v0
+...+ fmvm ,
fj
) = (u ,
fj ),
definindo u = f0 v0
+...+
fm vm , que é
uma função não nula, porque as funções
fj
são linearmente independentes.
Assim, vTSv = (u ,
f0
)v0
+...+ (u ,
fm
)
vm = (u , f0v0
+...+ fm vm
) = (u, u) = || u ||2 > 0,
e concluímos que S é definida positiva, e é
obviamente simétrica (no caso de ser considerado um produto interno
nos números complexos, a matriz seria hermitiana e ainda definida
positiva).
Exemplo: No caso de considerarmos a aproximação
através de funções polinomiais,
temos como funções base, f0
= 1, ... ,fm = xm, e assim
obtemos:
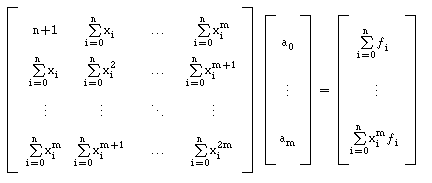
Observações:
podemos reparar que se trata de um produto na forma XTX ,
em que X é a matriz (n+1) x (m+1) :
| X = | é
ê ê ë |
|
ù
ú ú û |
A única diferença existente, face ao caso discreto, está na norma e no produto interno :
| || u ||2 = | b
ó õ a |
u(x)2 dx |
| ( u, v ) = | b
ó õ a |
u(x) v(x) dx |
Tudo se deduz de forma semelhante, e obtemos também um sistema normal, cuja única diferença está no significado dos produtos internos.
Exemplo:
No caso em que consideramos como funções base, os polinómios,
f0(x)=
1, ... ,fm(x)= xm, obtemos
agora o sistema normal
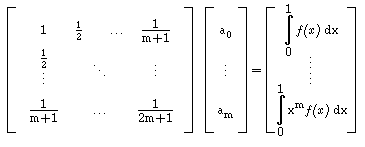
Esta matriz designa-se Matriz de Hilbert, e é extremamente mal
condicionada. Com efeito, já para m = 3 obtemos Cond1
= 28375, e para m = 4 já atinge 943656, continuando a crescer
fortemente! Temos, assim, problemas de condicionamento e consequentemente
de instabilidade numérica, para este tipo de matrizes.
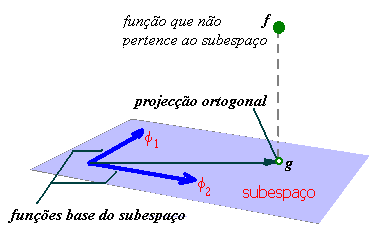
Através de um produto interno podemos falar na projecção ortogonal, e relembramos que, exigir:
Polinómios ortogonais
Consideramos uma situação um pouco diferente, no caso contínuo, em que pretendemos minimizar uma distância entre uma função f e uma função g, da forma g(x)=a1f1(x)+...+anfn(x), e em que essa distância é dada agora por
| || u ||w2 = | ó
õ |
b
a |
w(x) u(x)2 dx |
Notamos que a norma || .||w resulta do produto interno no intervalo [a, b] dado por
| ( u , v)w = | ó
õ |
b
a |
w(x) u(x) v(x) dx . |
Toda a dedução efectuada para o produto interno habitual (com w(x)=1) pode ser efectuada para este novo produto interno, obtendo também um sistema normal. De seguida iremos ver como podemos reduzir o sistema normal a um sistema com uma matriz diagonal, no caso em que pretendemos aproximar f por polinómios, usando funções base que são polinómios ortogonais.
Podemos obter os polinómios ortogonais aplicando o processo de
ortogonalização de Gram-Schmidt à base canónica
dos polinómios.
No entanto, podemos ver que há um processo mais simples, baseado
na seguinte fórmula de recorrência.
Teorema:
Dados dois polinómios q0 , q1
tais que (q0, q1)w
= 0, então a sucessão de polinómios definida pela
fórmula de recorrência
| qk+1 (x) = (x- | (x qk
, qk )w
|| qk ||w2 |
) qk(x) - | || qk ||w2
|| qk-1 ||w2 |
qk-1(x) |
Observação:
Para simplificar, considerámos os polinómios na forma
qk+1 (x) = c0 q0(x)+
... + ck qk(x) + qk(x)x
o que condiciona a escolha da constante do monómio de grau
k+1 a ser igual ao valor considerado em q1.
Poderíamos ter considerado, mais geralmente,
qk+1 (x) = c0 q0(x)+
... + ck qk(x) + ck+1
qk(x)x
mas isso apenas altera o valor dos polinómios por uma constante,
o que em nada influi na ortogonalidade.
Exemplos:
1 - Polinómios de Legendre (w(x)=1, no intervalo
[-1,1])
Consideramos w(x)=1 e começando com
P0(x) = 1, P1(x) = x
temos (P0,P1) = 0, e como (P0,P0)
= 2, (P1,P1) = 2/3, (x P1,P1)
= 0, obtemos
P2(x) = (x- 0)P1(x)-1/3
P0(x) = x2 - 1/3.
De forma semelhante, poderíamos obter P3(x)
= x3 - (3/5)x, etc...
Calculando (Pk , Pk) e (xPk ,
Pk) obteríamos a fórmula de recorrência
| Pn+1(x) = | (2n+1) x Pn(x) - n Pn-1(x)
n+1 |
| P0(x) = 1, | P1(x) = x, | P2(x) = (3x2 - 1)/2, | P3(x) = (5x3-3x)/2, ... |
2 - Polinómios de Chebyshev (w(x) = 1/ Ö(1-x2),
no intervalo [-1,1])
Consideramos agora w(x) = 1/ Ö(1-x2)
e começamos com T0(x) = 1, T1(x)
= x.
Da mesma forma, com constantes apropriadas, podemos deduzir
| Tn+1(x) = | 2 x Tn(x) - Tn-1(x) |
| T0(x) = 1, | T1(x) = x, | T2(x) = 2x2 - 1, | T3(x) = 4x3-3x, ... |