\(x^2+y^2 \lt 1 \;;\; x^2+z^2 \lt 1 \;;\; y^2+z^2 \lt 1\)

Cortes perpendiculares ao eixo \(Oz\)

Da definição, é claro que \( |z| \lt 1.\) Também é claro que \[|x| \lt \sqrt{1-z^2}\;;\; |y| \lt \sqrt{1-z^2}\] e, portanto, por um lado, \[x^2+y^2 \lt 2(1-z^2)\] e, por outro, \[x^2+y^2 \lt 1.\]

Assim, há dois casos a considerar: ou \(|z| \lt \frac{\sqrt{2}}{2}\) ou \(\frac{\sqrt{2}}{2} \lt |z| \lt 1.\)

Para o caso em que \(|z| \lt \frac{\sqrt{2}}{2},\) o correspondente corte é definido por \[x^2+y^2 \lt 1 \;;\; |x| \lt \sqrt{1-z^2}\;;\; |y| \lt \sqrt{1-z^2},\] tal como se mostra na figura seguinte:

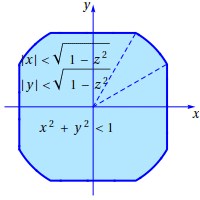
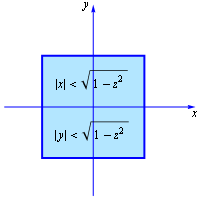
Para o caso em que \(\frac{\sqrt{2}}{2} \lt |z| \lt 1,\) o corte correspondente é o quadrado dado por \[ |x| \lt \sqrt{1-z^2}\;;\; |y| \lt \sqrt{1-z^2},\] tal como se mostra na figura seguinte:

Cálculo do volume

Seja \(X\) o sólido e considerem-se os cortes \(C_1(z)\) e \(C_2(z)\), perpendiculares ao eixo \(Oz\): \[C_1(z)=\{(x,y): \, x^2+y^2 \lt 1 \;;\; |x| \lt \sqrt{1-z^2}\;;\; |y| \lt \sqrt{1-z^2}\}, \quad |z| \lt \frac{\sqrt{2}}{2}.\] \[C_2(z)=\{(x,y): \, |x| \lt \sqrt{1-z^2}\;;\; |y| \lt \sqrt{1-z^2}\}, \quad \frac{\sqrt{2}}{2} \lt |z| \lt 1.\] Pelo Teorema de Fubini, tem-se \[\begin{align}\vol_3(X) &=2\int_{0}^{\sqrt{2}/2} \vol_2(C_ 1(z))dz +\\ &+ 2\int_{\sqrt{2}/2}^{1} \vol_2(C_ 2(z))dz.\end{align}\] Note-se que basta considerar, em cada um dos cortes, apenas a parte correspondente ao primeiro quadrante.

No primeiro quadrante, o corte \(C_2(z)\) (Fig. 2) é um quadrado de lado \(\sqrt{1-z^2}\) e, portanto, \[\vol_2(C_2(z))=1-z^2.\]

No primeiro quadrante, o corte \(C_1(z)\) (Fig. 1) é a união de dois trângulos rectângulos de base \(z\) e \(\sqrt{1-z^2}\), respectivamente, e um sector circular de raio igual a 1 e ângulo igual a \(\dfrac{\pi}{2}-2\arcsen z\,\).

Note-se que \(\left(\sqrt{1-z^2},z\right)\) é o ponto de intersecção do arco de circunferência \(x^2+y^2=1\) com a recta \(x=\sqrt{1-z^2}\). Portanto, \[\vol_2(C_1(z))=z\sqrt{1-z^2}+\dfrac{\pi}{4}-\arcsen z.\] Assim, \[\begin{align}\vol_3(X) &=8\int_{0}^{\sqrt{2}/2}\left(z\sqrt{1-z^2}+\dfrac{\pi}{4}-\arcsen z\right)dz+\\ &+8\int_{\sqrt{2}/2}^{1}\left(1-z^2\right)dz.\end{align}\] Usando a mudança de variável, \(z=\sen t\), na terceira parcela do primeiro integral, obtém-se \[\begin{align}\vol_3(X) &=8\int_{0}^{\sqrt{2}/2}\left(z\sqrt{1-z^2}+\dfrac{\pi}{4}\right)dz+\\ &+8\int_{0}^{\pi/4}\!\!\!t\cos t \, dt+\\ &+ 8\int_{\sqrt{2}/2}^{1}\left(1-z^2\right)dz\end{align}\] e, portanto, \[\vol_3(X)=16-8\sqrt{2}.\]