Cortes. Rampa

Uma Rampa Parabólica

$0 < x < 1; 0 < y < 1; 0 < z < x^{2} + y^{2}$

Cortes perpendiculares ao eixo $O x$

Fixando $0 < x < 1$ , obtém-se: $0 < y < 1; 0 < z < x^{2} + y^{2} .$ Assim, os cortes perpendiculares ao eixo $O x$ terão a forma que se apresenta na figura seguinte.

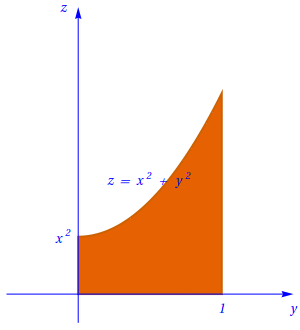
corte x — Fig. 1 Corte perpendicular a $O x$

Cortes perpendiculares ao eixo $O z$

Da definição, é claro que $0 < z < 2$ . O corte perpendicular ao eixo $O z$ é a intersecção do interior do quadrado, dado por $0 < x < 1; 0 < y < 1$ , com o exterior do círculo de raio $\sqrt{z}$ , com centro na origem e definido por $x^{2} + y^{2} > z$ . Assim, há dois casos a considerar: ou $0 < z < 1$ , ou $1 < z < 2$ .

Para $0 < z < 1$ , o corte encontra-se representado na figura seguinte:

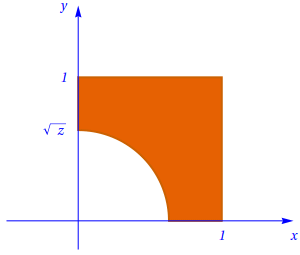
corte z — Fig. 2 Corte perpendicular a $O z$

Para $1 < z < 2$ , o corte encontra-se representado na figura seguinte:

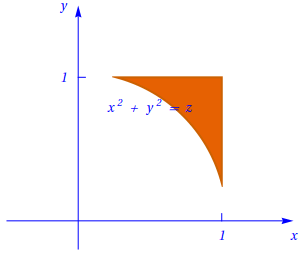
Cálculo do volume

Seja $X$ o sólido e considerem-se os cortes $C (x)$ , perpendiculares ao eixo $O x$ : $C (x) = {(y, z) : 0 < y < 1; 0 < z < x^{2} + y^{2}}, 0 < x < 1.$ Pelo Teorema de Fubini, tem-se $\begin{array}{rcl} {vol}_{3} (X) & = & \int_{0}^{1} {vol}_{2} (C (x)) d x \\ = & \int_{0}^{1} (\int_{0}^{1} (\int_{0}^{x^{2} + y^{2}} d z) d y) d x \\ = & \int_{0}^{1} (\int_{0}^{1} (x^{2} + y^{2}) d y) d x \\ = & \frac{2}{3} . \end{array}$