\(z+x^2 \lt 1 \;;\; z+y^2 \lt 1 \;;\;x \gt 0 \;;\; y \gt 0 \;;\; z \gt 0\)

Cortes perpendiculares ao eixo \(Ox\)

Da definição obtém-se: \[ \array{ 0 \lt z \lt 1-x^2, \text{ para } 0 \lt y \lt x \cr 0 \lt z \lt 1-y^2, \text{ para } x \lt y \lt 1.} \] Assim, os cortes perpendiculares ao eixo \(Ox\) têm a forma que se mostra na figura seguinte:

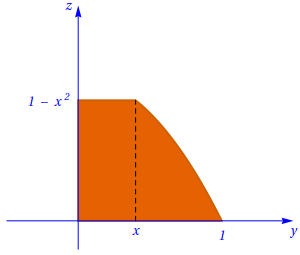
Cortes perpendiculares ao eixo \(Oz\)

Da definição, é claro que \(0 \lt z \lt 1\). Portanto, fixando a variável \(z\) neste intervalo, obtém-se \[0 \lt x \lt \sqrt{1-z} \;;\; 0 \lt y \lt \sqrt{1-z}.\] Assim, os cortes perpendiculares ao eixo \(Oz\) são quadrados, tal como se mostra na figura seguinte:

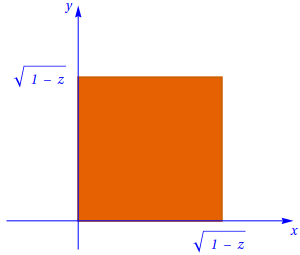
Cálculo do volume

Seja \(X\) o sólido e considerem-se os cortes \(C(z)\), perpendiculares ao eixo \(Oz\): \[C(z)=\left\{(x,y): \, 0 \lt x \lt \sqrt{1-z} \;;\; 0 \lt y \lt \sqrt{1-z}\right\}, \quad 0 \lt z \lt 1.\] Pelo Teorema de Fubini, tem-se \begin{eqnarray*} \vol_3(X) &=&\int_{0}^{1} \!\!\!\ \vol_2(C(z))dz \\ &=& \int_{0}^{1}\left(\int_{0}^{\sqrt{1-z}}\left(\int_{0}^{\sqrt{1-z}}dx\right)dy\right)dz \\ &=&\int_{0}^{1} \!\!\!\left(1-z\right)dz \\ &=& \frac 1 2. \end{eqnarray*} Note-se que o corte \(C(z)\) é um quadrado, tal como se mostra na Fig. 2. Então \[\vol_2(C(z))=(\sqrt{1-z})^2=1-z\] e, portanto, \[\vol_3(X)=\int_{0}^{1}\!\!\! \left(1-z\right)dz= \frac 1 2.\]